|
|
|
![]()
As we know from Hofstadter, the nucleon have hard core with a radius of 0.2 fermi surrounded by a meson cloud of radius 1.4 fermi. (Roughly !) Because of the impenetrability of the core the nuclei must look like almost spherical molecules with a covalent binding via a common pion cloud and the cores in the role nuclei. Consequently the nucleons are keeping some "individuality", masked partially by other terms of individual (two nucleon potential) or collective interactions of the nucleus as whole. It can be instructive to start modeling the nucleus as an almost spherical ensemble of impenetrable spheres. This model is constructed shell by shell, reaching a maximum of density when a shell is closed. The number of balls closing a shell can be interpreted as a "magic numbers". Comparing these numbers with the experimental results we are obtaining information of the effect of the other interaction terms, of course the most interesting places are that with large discrepancies. We can then add correction terms to fit the measured parameters of the nuclei.
How looks the model ?
|
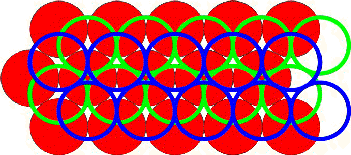
Let a plane layer of spheres, the red one. Then we can place
the next layer in a compact mode (above or below) or in the green or in the blue position.
Then we fill a zone of space, layer by layer in this way. The next job is to choose the
center of the wanted globular ensemble. They are five possibilities. Centering:
Then we start to construct, shell by shell, the five families. At higher shells different families can do almost the same magic number, some kind of isomers. I have used a small old (like me) program ball, downloadable as ball03.zip. Unfortunately the case 5 was omitted, needs on some work on the Fortran source. Results in graphical form.
|