|
About Me
problem
ars poetica
a.) A coordinate system symmetric in the angular variables .
a01, a02, a03, a04, a05, a06 . Generalizing the trigonometric functions in a natural way, we can construct a coordinate system symmetric in the angular coordinates, but non-orthogonal, connected with the surface x3+y3+z3+3xyz=r3=const. This system have some interesting properties and suggests some interesting problems. One of the application is the kinematics and dynamics in terms of this system.

=============================================================
aa.) An application: generalizing the functions of the previous
article (a.) and applying its to the algebraic equations, a suspected general
method for solving these equations appears.
aa00, aa01, aa02, aa03
=============================================================
b.) The solution of the first order, quadratic ODE 
b01, b02 . The general solution is calculated by the method of Jules Drach, as a first step in solving some first order, quadratic ODE-s. The results are remarkable symmetrical.
c.) [?] Series solution of the first order, quadratic ODE 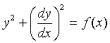
c01
d.) [?] Hunting a rule to explain the solution of the first order ODE 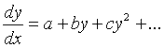
d01 A tentative to generalize a property of the Riccati equation.
dg.) A new, almost general, curvilinear coordinate system, the "potential" one
With a natural suplimentary condition, the general curvilinear coordinate system
moves in a completely symmetric pair, "lighting" a lot of properties.
dg11, dg12, dg21, dg22, dg3, dg41, dg42, dg5, dg61, dg62, dg7, References,
dga.) An example how the "engine" described in article dg. works in connection with the classical mechanics.
dga01,
dgb.) The second example use the coordinate system defined in article a. and leads to a slightly modified form of the dg. "engine".
dgb01,
dgc.) An alternate form of the classical dynamics.
dgc,
dgd.) Small remarks on the relativistic electrodynamics.
dgd,
=====================================================================
dge.) dge
dge,
dgf.) Rolling surface and geodesics.
dgf,
=====================================================================
=====================================================================
dgg.) Non-holonomic surface.
dgg,
=====================================================================
=====================================================================
dgh.) Trajectories-Geodesics.
dgh,
=====================================================================
=====================================================================
dgi.) Minimal surface.
dgi,
=====================================================================
=====================================================================
dgk.) Integral formulas.
dgk,
=====================================================================
e.) A representation of numbers by prime numbers, the ?next? elementary function and a possible memory chip with a new structure, for compact, high precision representation of big numbers.
e01 A naive way to construct higher elementary functions, the first step and a possible application.
f.) Alternate method to fit some experimental z=f(x,y) data, with unknown analytical comportment, by an empirical function (a surface).
f01 If in a small interval the right line is a good approximation for any curve, what happen between two small intervals. The result is a function non-continuous in derivatives, hard for calculating manually, but very easy for a computer.
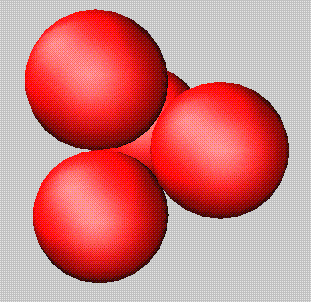
g.) Globular ensembles of impenetrable spheres and the structure of the nuclei.
Download ball03.zip
h.) Two ?cosmological? remarks and an optimized measurement.
i.) Motion under the non-central potential 
containing the central, newtonian potential as a subcase.
i01 A good example for the motion under a non-central potential, to form an image what effect have the non-centrality, compared with a central "neighbour".
==========================================================
j.) j01 The general plane problem in the classical dynamics. Where is the second integral ?
j02 Details on "Where is the second integral in the plane problem?"
j03 The plane problem in an alternate form of the dynamics.
j04, j05,
================================================================================
jk.) A step to non-linear potentials in the classical mechanics and the co-linear three-body problem.
jk01,
==========================================================
================================================================================
jka.) More on the colinear three-body problem.
jkaBIS.) More on the colinear three-body problem.Some details.
================================================================================
================================================================================ ================================================================================
k.) Around the collinear three-body problem in the classical mechanics.
k01,
==========================================================
================================================================================
ka.) Presumptive solution of the plane three-body problem in the classical mechanics.
ka,
==========================================================
================================================================================
kb.) More on the plane three-body problem. A way of solving?
================================================================================
================================================================================
|
 =====================================================================================================================================================
=====================================================================================================================================================
![]()